Using surnames to create break-out groups
If you facilitate meetings on a regular basis you usually have situations where you need to create ‘break-out groups’. While sometimes these are pre-assigned, very often they are random groups of people that are roughly equal in size.
The problem facilitators run into is that while they know the number of people they may want in each group, they don’t always know how many in total are actually going to show up to the session.
One solution is having participants count off by the number of groups you want. So if you want 5 groups you have people count off by 5s going around the room (1,2,3,4,5, and then repeat 1,2,3,4,5, etc).
The downside of this approach is that it takes a fair amount of time in a larger group and if they are not arranged in a classroom style it can be awkward to tell who is “up” to say their number. Also, I can’t tell you the number of times people have asked “what is my number again?” after uttering it seconds before.
One solution is to divide people by last name. In this way you can eyeball the group in attendance and just divide them up by the number of groups you want or the number in each group you want.
Unfortunately, last names are not randomly distributed in the United States. In fact, looking at the distribution of last names that appear at least 100 time or more in 2010 US Census it looks like this:
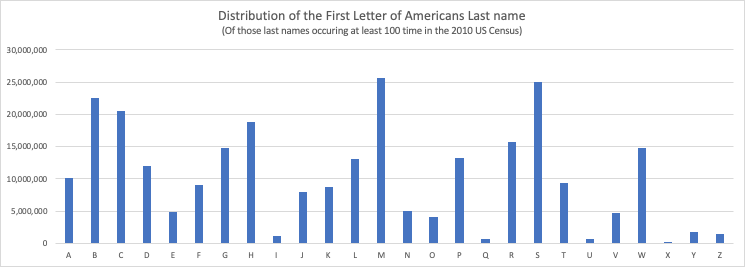
As you can see Millers, Smiths, Browns, Clarks, and Williams dominate, while Ingrams, Quinns, Underwoods, Xiongs, and Zimmermans are relative rarities. To solve for this we can divide them into n-tiles and if we trust our 200 level statistics class, we can then infer that this distribution will exist in the population in your next destination.
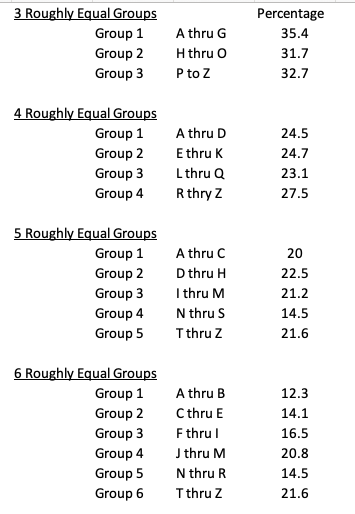
You can use the tables below to divide your groups into 3, 4, 5, or 6 roughly equal groups. Since the letter breaks are exactly on the desired percentile cut point, they are not exact. This also make dividing groups larger than 6 a bit dicey.
Now, there will be exceptions to this. For example, locations that are heavily skewed to one ethnicity may not conform to this distribution. It also not likely work in countries outside of the United States as well. That being said, it should work fairly well in most circumstance. Good luck and let me know how it goes!



